Looking at a map of our sky, we see immediately that galaxies are not randomly distributed in our universe: they are grouped in clusters and filaments. This pattern in the clustering of galaxies, called large-scale structure, is rich in information about the fundamental laws governing the evolution of our universe. In particular, by studying the properties of the large-scale structure, we can probe the law of gravitation as well as the nature of the mysterious dark matter and dark energy, that are believed to account for 95 percent of the universe’s content. In my research I study the large-scale structure in two distinct but complementary regimes: the large-scale relativistic regime, and the small-scale non-linear regime. I devote also part of my time to the problematic of primordial magnetic fields. I am specifically interested in studying their impact on the CMB.
Large-scale structure in the relativistic regime
At small scales, the growth of structure is very well described by Newton’s theory of gravitation. At large scales however, General Relativity generates novel contributions to the observed distribution and shape of galaxies. Light propagation is indeed affected by the geometry of the universe, generating distortions in the observed image of our sky. These distortions add new relativistic contributions to the standard Newtonian description of our universe.
Understanding these relativistic distortions is important from two points of view. First, challenging galaxy surveys have been planed for the next decades, with the goal to observe almost the whole sky. These surveys will open a new window on our universe, allowing us to test for the first time the laws of gravity at very large distance, in the regime where they truly differ from Newton’s laws. To interpret these future data correctly, it is crucial to have a consistent description of large-scale structure observables in the framework on General Relativity. In this optic, I have calculated the relativistic corrections to the luminosity distance (Bonvin, Durrer and Gasparini 2006, Bonvin, Durrer and Kunz 2006), the cosmic convergence (Bonvin 2008) and the cosmic shear at second order (Bernardeau, Bonvin and Vernizzi 2010, Bernardeau, Bonvin, Van de Rijt and Vernizzi 2012). I have also investigated the impact of relativistic effects on the number count of galaxies (Bonvin and Durrer 2011) and on the 21cm intensity mapping (Hall, Bonvin and Challinor 2013).
Second, having a completely relativistic description of our sky is crucial because it gives us access to new information about the properties of our universe. For example, gravitational redshift, which describes the effect of a gravitational potential on the photon’s energy, generates distortions in the number count of galaxies. Contrary to the Newtonian contributions, these distortions probe the time component of the metric. Measuring directly gravitational redshift in large-scale structure opens consequently the door to novel and model-independent tests of gravity, like for example, testing the validity of Euler equation at large scales. With this in mind, I have developed a new method to isolate relativistic effects in the two-point function of galaxies (Bonvin, Hui and Gaztanaga 2014). The key point of this method is to look for anti-symmetries in the two-point cross-correlation function between two distinct populations of galaxies.
Large-scale structure in the non-linear regime: phase correlations
Understanding the large-scale structure of the universe requires to understand the statistical properties of the matter density field. In Fourier space, the density field is characterised by an amplitude and a phase. The satellite Planck has recently observed that, up to a very good precision, the initial density field is Gaussian. This has the strong consequence that, in the primordial universe, all the information is contained in the amplitude of the density field. The phases are randomly distributed and uncorrelated. The linear gravitational evolution of the density preserves this property, so that in the linear regime, the power spectrum (or equivalently the real-space two-point correlation function) is sufficient to completely characterise the properties of the large-scale structure.
At small scales however, the density field evolves non-linearly and becomes non-Gaussian. The consequence is that the phases of the density field become non-uniformly distributed and correlations emerge. The power spectrum is not sufficient anymore to encode all the information in the non-linear regime and new statistical measures have to be considered. With my collaborators we have constructed a novel estimator, the line correlation, which probes directly correlations between the phases (Obreschkow, Power, Bruderer and Bonvin, 2013). This estimator is particularly well adapted to measure the filamentarity of the large-scale structure and the properties of dark matter in the non-linear regime.

In perturbation theory, the line correlation can be expressed in terms of the linear power spectrum and the non-linear coupling kernel (Wolstenhulme, Bonvin and Obreschkow, 2014). This shows that the line correlation provides a direct and optimal way to measure the non-linear properties of gravitational evolution. In addition, the line correlation has the strong advantage of being independent of linear bias. We are currently studying the improvements that the line correlation brings with respect to the bispectrum in measuring various cosmological parameters.
You can download here the code to calculate the line correlation.
Primordial magnetic fields
Besides my interest for large-scale structure, I am also fascinated by magnetic fields. Magnetic fields are ubiquitous in the universe: they have been observed in galaxies, clusters of galaxies and recently in voids, but their generation mechanism is still unknown. Their large correlation length and their presence in voids suggest that they may have been produced in the early universe, either during inflation, or during a phase transition shortly after inflation.
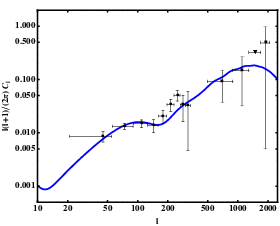
If this is the case, they are excepted to contribute to fluctuations of the Cosmic Microwave Background and to leave a distinct imprint (providing that their amplitude is sufficiently large) on the temperature and polarisation power spectra (Bonvin and Caprini 2010, Bonvin, Caprini and Durrer 2012, Bonvin, Caprini and Durrer 2013).
Since magnetic fields have a non-zero anisotropic stress containing a scalar, vector and tensor part, they contribute to the CMB power spectrum in a different way than radiation. For example, magnetic fields generate B-modes in the polarisation power spectrum. They could therefore be at the origin of the B-modes observed by BICEP2 (Bonvin, Durrer and Maartens 2014).
